Deret aritmatika adalah deret yang diperoleh dari penjumlahan suku-suku barisan aritmatika.

• Rumus suku ke-n:

\[ a_n = a_1 + (n-1)d \]

Di mana:

• \(a_n\) = suku ke-n
• \(a_1\) = suku pertama
• \(d\) = beda antar suku
• \(n\) = nomor suku
• Rumus jumlah n suku pertama:

\[ S_n = \frac{n}{2}(2a_1 + (n-1)d) \]

atau

\[ S_n = \frac{n}{2}(a_1 + a_n) \]

• Sisipan suku dalam deret aritmatika:

Jika diketahui dua suku \(a_m\) dan \(a_n\), maka jumlah suku antara keduanya adalah:

\[ \text{Jumlah suku sisipan} = n - m - 1 \]

Dan nilai suku sisipan dapat dicari dengan rumus suku ke-n yang sesuai.

• Suku tengah:

Jika \(n\) ganjil, suku tengah adalah suku ke-\( \frac{n+1}{2} \), yaitu:

\[ a_{tengah} = a_{\frac{n+1}{2}} = a_1 + \left(\frac{n-1}{2}\right)d \]

Jika \(n\) genap, rata-rata dua suku tengah yaitu:

\[ \frac{a_{\frac{n}{2}} + a_{\frac{n}{2}+1}}{2} \]

• Contoh:

1. Diberikan deret aritmatika \(2, 5, 8, 11, \ldots\), tentukan suku ke-10.

\[ a_{10} = 2 + (10-1) \times 3 = 2 + 27 = 29 \]

2. Hitung jumlah 15 suku pertama dari deret \(4, 7, 10, 13, \ldots\).

\[ S_{15} = \frac{15}{2} \left(2 \times 4 + (15-1) \times 3 \right) = \frac{15}{2}(8 + 42) = \frac{15}{2} \times 50 = 375 \]

Deret geometri adalah deret yang diperoleh dari penjumlahan suku-suku barisan geometri.

• Rumus suku ke-n:

\[ a_n = a_1 \times r^{n-1} \]

Di mana:

• \(a_n\) = suku ke-n
• \(a_1\) = suku pertama
• \(r\) = rasio (perbandingan antar suku)
• \(n\) = nomor suku
• Rumus jumlah n suku pertama:

\[ S_n = a_1 \frac{r^n - 1}{r - 1} \quad (r \neq 1) \]

• Sisipan suku dalam deret geometri:

Jika diketahui dua suku \(a_m\) dan \(a_n\), suku sisipan dapat dicari dengan rumus:

\[ a_k = a_m \times r^{k-m} \]

• Suku tengah:

Jika \(n\) ganjil, suku tengah adalah suku ke-\( \frac{n+1}{2} \).

Jika \(n\) genap, suku tengah adalah akar dari hasil kali dua suku tengah:

\[ \sqrt{a_{\frac{n}{2}} \times a_{\frac{n}{2}+1}} \]

• Contoh:

1. Deret \(3, 6, 12, 24, \ldots\), tentukan suku ke-7.

\[ a_7 = 3 \times 2^{6} = 3 \times 64 = 192 \]

2. Hitung jumlah 5 suku pertama deret \(5, 15, 45, 135, \ldots\).

\[ S_5 = 5 \times \frac{3^5 - 1}{3 - 1} = 5 \times \frac{243 - 1}{2} = 5 \times 121 = 605 \]

Deret tak terhingga adalah deret dengan jumlah suku yang tak terbatas, biasanya untuk deret geometri dengan \(|r| < 1\).

• Jumlah deret tak terhingga:

\[ S = \frac{a_1}{1 - r}, \quad \text{dengan } |r| < 1 \]

• Contoh soal:

1. Tentukan jumlah deret tak terhingga \(2 + 1 + \frac{1}{2} + \frac{1}{4} + \ldots\)

\[ S = \frac{2}{1 - \frac{1}{2}} = \frac{2}{\frac{1}{2}} = 4 \]





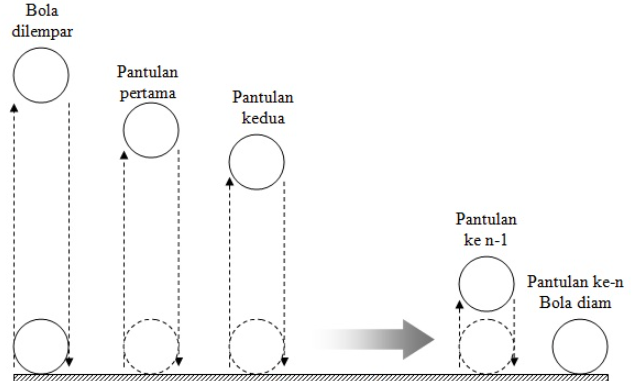
2. Sebuah bola memantul dengan tinggi awal 8 m dan setiap pantulan ketinggiannya menjadi setengah dari pantulan sebelumnya. Hitung total jarak yang ditempuh bola sampai berhenti.

Bola turun 8 m ke tanah, lalu naik \(8 \times \frac{1}{2} = 4\) m, lalu turun 4 m, naik 2 m, turun 2 m, dan seterusnya.
Total jarak \(S\) adalah:

\[ S = 8 + 2 \times \left(4 + 2 + 1 + \cdots \right) \]

Deret naik dan turun membentuk deret geometri tak terhingga dengan \(a_1=4\) dan \(r=\frac{1}{2}\). Maka:

\[ S = 8 + 2 \times \frac{4}{1 - \frac{1}{2}} = 8 + 2 \times 8 = 8 + 16 = 24 \]

a. Deret Aritmatika

1. Seorang petani menanam pohon secara bertahap. Pada tahun pertama ia menanam 10 pohon, tahun kedua 15 pohon, tahun ketiga 20 pohon, dan seterusnya. Berapa pohon yang ditanam pada tahun ke-8?
   Jawaban:
   \[ a_8 = 10 + (8-1) \times 5 = 10 + 35 = 45 \]


2. Sebuah mobil melaju dengan kecepatan awal 40 km/jam, setiap jam kecepatannya bertambah 5 km/jam. Berapakah kecepatan mobil pada jam ke-6 dan berapa total jarak yang ditempuh selama 6 jam?
   Jawaban:
   Kecepatan pada jam ke-6: \[ a_6 = 40 + (6-1) \times 5 = 40 + 25 = 65 \text{ km/jam} \] Total jarak: \[ S_6 = \frac{6}{2} (40 + 65) = 3 \times 105 = 315 \text{ km} \]

b. Deret Geometri

1. Sebuah bakteri membelah diri setiap jam, mulai dari 3 bakteri. Jika jumlah bakteri menjadi 3, 6, 12, 24, ... berapa banyak bakteri pada jam ke-7?
   Jawaban:
   \[ a_7 = 3 \times 2^{6} = 3 \times 64 = 192 \]


2. Sebuah investasi awal Rp 1.000.000 menghasilkan bunga 10% per tahun dan bunga tersebut selalu diinvestasikan kembali. Berapa total uang setelah 5 tahun?
   Jawaban:
   \[ S_5 = 1.000.000 \times \frac{1.1^5 - 1}{1.1 - 1} = 1.000.000 \times \frac{1.61051 - 1}{0.1} = 1.000.000 \times 6.1051 = 6.105.100 \]